COMPLEMENTO DE UN GRAFO
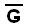 de un grafo dado G es un grafo cuyo conjunto de vértices es el mismo que el del grafo G y si dos vértices están relacionados en el complemento es porque no lo están en G, es decir, el conjunto de vértices V(
de un grafo dado G es un grafo cuyo conjunto de vértices es el mismo que el del grafo G y si dos vértices están relacionados en el complemento es porque no lo están en G, es decir, el conjunto de vértices V( ) = V(G) y (u R v ) en
) = V(G) y (u R v ) en 
- Dibujar el corresp. grafo completo
 , con n=lVl
, con n=lVl- Eliminar de
 las aristas {u,v} pertenecientes a G
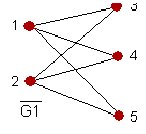
las aristas {u,v} pertenecientes a GEjemplo : Complementario ( ver la figura anexa)

2º marcar las aristas de G
3º Eliminarlas
COROLARIO 1: Si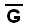 es el grafo complemento de G, entonces:
es el grafo complemento de G, entonces:
Demostración:
La parte a) del corolario es una consecuencia inmediata de la definición de grafo complementario. Para la parte b) sabemos, por definición, que las líneas que están en G no pueden estar en su complemento, por lo tanto si a todas las posibles líneas del grafo ![]()
(p(p -1)/2 líneas) le restamos las líneas que tiene G obtenemos el número de líneas que debe tener el grafo complementario  .
.
Ejemplo 1:
Observemos que el grafo G2 del ejemplo 1, o sea, el ciclo  es isomorfo con su grafo complementario, G2
es isomorfo con su grafo complementario, G2
 2. Cuando esto ocurre, se dice que G2 es un Grafo Autocomplementario.
2. Cuando esto ocurre, se dice que G2 es un Grafo Autocomplementario.
Otro ejemplo es
siendo éste el grafo autocomplementario con menor número de vértices.
TEOREMA 2.1: Todo grafo autocomplementario tiene 4n ó 4n+1 vértices, siendo n un número entero, es decir, el número de vértices de un grafo autocomplementario es 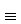 0 ó 1(módulo 4).
0 ó 1(módulo 4).
Demostración:
Basándonos en el Corolario 1, sabemos que 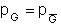 y
y  , pero como G
, pero como G 
 , entonces,
, entonces, .
.
Como p y  son números enteros consecutivos, el máximo común divisor entre ambos números es 1. Luego, 4 es divisor de p ó de
son números enteros consecutivos, el máximo común divisor entre ambos números es 1. Luego, 4 es divisor de p ó de  , es decir, p = 4n ó p = 4n+1, n
, es decir, p = 4n ó p = 4n+1, n  N.
N.
OBSERVACION 2.1.1: El Teorema 2.1 proporciona una condición necesaria, pero no suficiente, es decir que hay grafos con p = 4n ó p = 4n+1 vértices sin ser autocomplementarios. Por ejemplo, el grafo complementario de un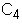 es el
es el  .
.
Nota:
El siguiente problema, muy conocido por los estudiantes que presentan exámenes de admisión a las universidades o participan en las Olimpíadas Matemáticas, es muy típico en la Teoría de Grafos y uno de sus enunciados es:
- Demostrar que en cualquier reunión social, en la que participan seis personas, siempre existen tres personas que se conocen entre sí, o tres que no.
Esta situación se puede representar por medio de un grafo G con seis vértices, en el cual los vértices representan a las personas y existe una relación R entre los vértices (personas) si esas dos personas se conocen entre sí. Entonces el problema se reduce a demostrar que G tiene tres vértices que son adyacentes entre sí; o bien posee tres vértices que no lo son. Pensando así el problema tenemos el siguiente enunciado equivalente:
TEOREMA 2.2 (Ramsey) Todo grafo G con seis vértices es tal que G ó  contiene un triángulo.
contiene un triángulo.
Demostración:
Sea v un vértice en G con . Si G es un
. Si G es un , entonces
, entonces  y
y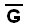 contiene triángulos. Si G es un
contiene triángulos. Si G es un  , entonces
, entonces contiene un
contiene un  , en el cual todo vértice de está unido a los demás vértices del grafo ; por lo tanto,
, en el cual todo vértice de está unido a los demás vértices del grafo ; por lo tanto,  tiene triángulos. Análogamente, si G contiene tres vértices aislados,
tiene triángulos. Análogamente, si G contiene tres vértices aislados,  entonces
entonces  tiene, por lo menos, el triángulo
tiene, por lo menos, el triángulo  . Por lo tanto, podemos suponer, sin perder generalidad, que existen tres vértices
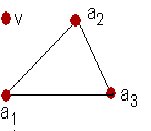
. Por lo tanto, podemos suponer, sin perder generalidad, que existen tres vértices  adyacentes a un vértice v en G; o sea, G contiene el subgrafo representado en la figura adjunta.
adyacentes a un vértice v en G; o sea, G contiene el subgrafo representado en la figura adjunta.

Si cualesquiera dos de los  son adyacentes, entonces G posee un triángulo cuyo tercer vértice es v. Si, por el contrario, los no están relacionados entre sí, entonces
son adyacentes, entonces G posee un triángulo cuyo tercer vértice es v. Si, por el contrario, los no están relacionados entre sí, entonces  tiene el subgrafo que se ve a continuación
tiene el subgrafo que se ve a continuación




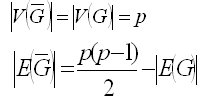



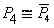

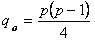

0 Comments:
Post a Comment
<< Home