GRAFOS CONEXOS
Ej:
A menudo se presenta el problema de una fábrica que posee varias sucursales en diferentes ciudades y se desea poder ir de una sucursal a otra sin dejar de visitar ninguna. Cuando esto es posible se habla de que el grafo asociado a las diferentes sucursales es conexo. Para entender este concepto, es necesario dar algunas definiciones que nos describan qué significa ir de un vértice a otro.
Un recorrido (vo, vn) de un vértice vo a un vértice vn en un grafo G es un subgrafo de G que consiste en una sucesión alternada de vértices y líneas, comenzando con vo (que se llama vértice inicial) y terminando en vn (que se llama vértice final). Dicha sucesión finita, vox1v1x2 ...xnvn, presenta la propiedad de que para toda i, 1< size="1">i son vi - 1 y vj.

FIG 3.1
Un recorrido sería: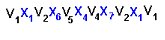
Si un recorrido es tal que ninguna de sus líneas aparece repetida, dicho recorrido lo denominaremos ruta o trazado. Por ejemplo:
En la FIG 3.1
Una ruta o trazado podría ser 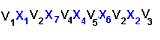
En el caso de que el recorrido sea tal que ningún vértice aparezca repetido, diremos que se trata de un camino o sendero. Por ejemplo:
En la FIG 3.1
Un camino o sendero podría ser

En el caso de que el recorrido sea tal que ningún vértice aparezca repetido, diremos que se trata de un camino o sendero. Por ejemplo:
En la FIG 3.1
Un camino o sendero podría ser
Cuando vo = vn, diremos que el recorrido es cerrado; en caso contrario, lo llamaremos recorrido abierto. Ahora bien, si el recorrido es cerrado y todos los vértices son distintos, excepto el inicial vo y el final vn que son iguales, tenemos un ciclo. También podemos decir que un ciclo es un camino cerrado.
OBSERVACION 3.1.1: Todo ciclo es una ruta, y por lo tanto un recorrido.
Denotaremos a los ciclos como Cp, donde p>3 o p = 3. Cuando p = 3, el ciclo C3 es llamado triángulo y para p > 3 los ciclos Cp son llamados p-ágonos.
OBSERVACION 3.1.2: Cuando no haya confusión en los recorridos, rutas, caminos o ciclos, podemos omitir las líneas y dejar sólo los vértices. Al menos para nuestros grafos simples esto es válido. Así, en la Fig. 3.1 v1v2v3v4v5v1 representa el pentágono C5.
Para hablar de grafo conexo, diremos que dos vértices u, v V(G) están "conectados" si existe un camino (u, v) en G. Entonces, es fácil ver que la conexión es una relación de equivalencia en V(G).
Para ver que la relación de ser conexo es simétrica, supongamos que u, v pertenecen a V(G) y u distinto de v están conectados, entonces (por definición) sabemos que existe un camino (u, v) que relaciona a u con v. Pero v está en relación con u porque si existe un camino (u, v), también existe un camino (v, u), (ver fig. 3.2 a)).
En forma trivial podemos considerar que el vértice u está conectado consigo mismo; es decir, la relación de ser conexo también es reflexiva. Para ver que es transitiva, consideramos que u y v están conectados y v y w también, con u distinto de w. Entonces, existe el camino (u, v) y el camino (v, w). Por lo tanto, existe el camino (u, w). (Ver fig. 3.2 b)).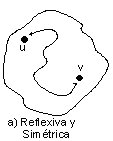
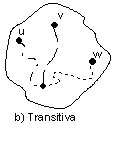
Fig. 3.2
Sabemos que toda relación de equivalencia separa al conjunto V(G) en subconjuntos no vacíos V1, V2, V3, ... , Vk, donde la relación es tal que dos vértices u y v están conectados si y sólo si ambos, u y v, pertenecen al mismo conjunto Vi. Por otra parte, los subgrafos G[V1], G[V2], ... , G[Vk] son llamados componentes de G. Ahora, si G tiene exactamente una componente, es decir, k = 1, el grafo G es conexo. Denotaremos por k(G) al número de componentes conexas o simplemente componentes del grafo G.
Ejemplo 2: El grafo G de la fig. 3.3 tiene k(G) = 5.
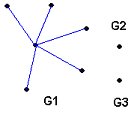

Fig. 3.3
Observe que en la fig. 3.3 no existe (por ejemplo) un camino entre los vértices de la componente G1 y los de la componente G4. Deducimos de aquí que un grafo G es conexo si y sólo si todo par de vértices de G puede ser unido por un camino.
TEOREMA 3.1 Sea G un grafo simple con p vértices. Si G tiene k componentes, entonces el número q de líneas de G satisface: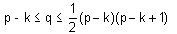
Demostración:
Para demostrar que q es mayo o igual a p - k, usaremos inducción sobre el número de líneas de G. Para los Np el resultado es trivial, ya que p - k = 0 y q = 0. Si G contiene, a saber qn líneas que lo hacen conexo, al eliminar cualquiera de ellas aumentaremos en uno el número de componentes conexas del grafo G, y el grafo resultante seguirá teniendo p vértices pero k+1 componentes. Entonces, por hipótesis inductiva qn es mayor o igual que p - (k + 1), de donde podemos deducir automáticamente que qn es mayor o igual a p - k.
Para demostrar el otro lado de la desigualdad, supongamos que cada componente de G es un grafo completo. Entonces, podemos asumir que existen por lo menos dos componentes Ci y Cj con pi y pj vértices respectivamente, donde:

Si reemplazamos Ci y Cj por grafos completos con pi + 1 y pj - 1 vértices, luego el número total de vértices no se altera, pero el número de líneas aumenta de la siguiente manera:
Entonces, es obvio que para obtener el máximo número de líneas, G debe ser un grafo completo con p - k + 1 vértices y k - 1 vértices aislados, luego es obvio que el número total de líneas de G va a satisfacer la desigualdad,
COROLARIO 1: Cualquier grafo simple con p vértices y más de líneas, es conexo.
Tal como su nombre lo indica, los recorridos implican costos (por ejemplo, cuando se habla de problemas de transporte) y por lo tanto se hace necesario estudiar el concepto de longitud de un recorrido. En particular, definiremos lo que es la longitud de un camino como el número de líneas que contiene el camino. Así, el camino (vo, vn) = vox1v1x2 ... xnvn tiene longitud n.
Llamaremos cintura de un grafo G, cin(G), a la longitud de un ciclo más corto, si es que existe y circunferencia, cir(G), a la longitud de su ciclo más largo.
Ejemplo 3: El grafo que se muestra en la fig. 3.4 tiene cin(G) = 4 y cir(G) = 10. El cin(G) es la longitud del C4 formado por un subconjunto de vértices de G, y el cir(G) está dado por las líneas punteadas que aparecen en el grafo. 
Fig 3.4
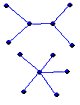
OBSERVACION 3.1.3: Los términos de cintura y de circunferencia no están definidos para grafos que no tienen ciclos. Un caso muy particular de grafos que no presentan ciclos, pero sí son conexos, son los llamados árboles.
Ejemplo 4: La familia de árboles no isomorfos con seis vértices.

Fig 3.5
Se llama distancia, d(u, v), entre dos vértices u y v de un grafo G, a la longitud del camino más corto existente; en caso contrario, se dice que d(u,v) = infinito. La excentricidad de un vértice v perteneciente a G, que denotaremos e(v), es la máxima distancia d(u,v) entre todos los u pertenecientes a G. Llamaremos diámetro, d(G), a la máxima excentricidad de todos los vértices de G; y radio de G, denotado r(G), a la mínima excentricidad de todos los vértices de G.
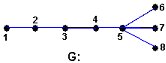
Ejemplo 5: Hallar el diámetro y el radio del grafo G de la fig. 3.6.

Fig. 3.6
e(v1) = 3; e(v2) = 2; e(v3) = 2; e(v4) = 3; e(v5) = 3 e(v1) = e(v4) = e(v5) = 3 y e(v2) = e(v3) = 2, entonces, d(G) = 3 y r(G) = 2.
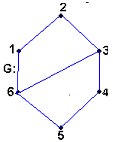
En algunos grafos conexos se cumple que la excentricidad de un vértice v es igual al radio del grafo G, e(v) = r(G), en este caso se dice que v es un vértice central de G. Al conjunto de todos los vértices centrales lo llamaremos centro de G, y se denotará C0(G). Así, para el ejemplo 8, tenemos que para G se cumple que e(1) = 5; e(2) = 4; e(3) = 3; e(4) = 3; e(5) = 4; e(6) = 5; e(7) = 5; e(8) = 5, por lo tanto, el r(G) = 3, luego C0(G) = {3, 4}.
OBSERVACION 3.1.4: Para el caso de la estrella, , con n mayor o igual a 2 se tiene que C0(G) está formado por el único vértice de valencia n.
Ejemplo 6: En la fig. 3.7 se tiene e(1) = e(3) = 3 y e(2) = e(4) = e(5) = e(6) = 4; por lo tanto, C0(G)={1, 3}.
Más adelante, cuando se estudie el concepto de "peso de un grafo", volveremos a encontrar la idea de centro de un grafo.
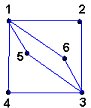
A continuación veremos la aplicación del concepto de distancia para definir una nueva familia de grafos. El cuadrado de un grafo G, está definido como el grafo G al cuadrado, tal que
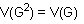 y dos vértices u, v G están relacionados en G al cuadrado si cumplen que d(u, v) es menor o igual a 2 en G. En general,
y dos vértices u, v G están relacionados en G al cuadrado si cumplen que d(u, v) es menor o igual a 2 en G. En general,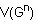 de un grafo G está definido como
de un grafo G está definido como
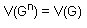
Y dos vértices u, v pertenecientes a G están relacionados en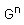 si y sólo si d(u, v) es menor o igual a n en G.
si y sólo si d(u, v) es menor o igual a n en G.
Ejemplo 7:
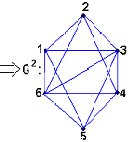
Fig 3.8
Claramente, si tenemos un grafo G = Kp , entonces también Gn = Kp para todo n mayor o igual a 2.
Ejemplo 8: Dado el grafo G de la fig. 3.8, hallar G al cubo.
Ejemplo 8: Dado el grafo G de la fig. 3.8, hallar G3 .
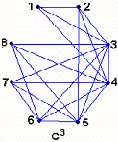
Fig 3.8
Note que en el grafo G3 las valencias de los vértices son v1 = 3; v2 = 4; v3 = v4 = 7; v5 = 6; v6 = v7 = v8 = 5; luego el grafo G3 tiene 21 líneas.
Observemos que en este ejemplo
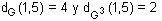 ¿Es posible encontrar una relación entre
¿Es posible encontrar una relación entre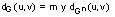
En efecto, para determinar 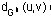
debemos considerar dos casos:
i)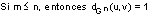
ya que los vértices u y v en G están a menor distancia que n.
ii) 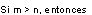
En efecto, sabemos que 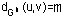
y a medida que aumenta la potencia de G, disminuye 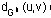
por lo tanto, si m > n debemos ver cuántas veces está contenido n en m y si no es exacta la división, entonces a su parte entera le sumamos uno.

0 Comments:
Post a Comment
<< Home