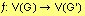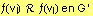INTRODUCCIÓN

Estamos dando inicio a una serie de Programas Educativos, utilizando los llamados blogs, las presentaciones en Power Point y más adelante algunos videos y material escrito a modo de Guías de Estudio.

El contenido básico lo hemos extraído del texto: Introducción a la Teoría de Grafos de Reinaldo Giudici Espinoza y Angeles Bris Lluch, editorial Equinoccio, Universidad Simón Bolívar, Caracas, Venezuela, 1997.

Esta idea surgió durante la enseñanza del curso Teoría de Grafos (Mat-349) que dicta el Prof. Giudici en el Instituto de Matemáticas de la Pontificia Universidad Católica de Valparaíso (IMA), 2006.

.

En esta primera etapa hemos trabajado los primeros tres capítulos del texto, anteriormente mencionado, y esperamos ir cubriendo todo el material que hay en dicho libro.

Este es un primer avance que entregamos a todos los interesados en la Teoría de Grafos, especialmente a los principiantes y esperamos que otros estudiantes del IMA se contagien en un futuro cercano.

El trabajo de creación de los blog ha sido realizado por el estudiante Claudio Cifuentes y han colaborado, por orden de Capítulo, los estudiantes:

• Capítulo I - Claudio Cifuentes y Giselle Mora (Capítulo I)
• Capítulo II - Andrea Olmedo (Capítulo II)
• Capítulo III - Lillibeth Elgueta (Capítulo III)
  
  

Reinaldo Giudici

Profesor Teoría de Grafos (MAT-349)

Reinaldo Giudici Espinoza

Profesor del Curso MAT-349 : "Introducción a la Teoría de Grafos", en la Pontificia Universidad Católica de Valparaíso (PUCV)

Claudio Cifuentes Marchant

Estudiante de Pedagogía en Matemáticas, 5to año, Pontificia Universidad Católica de Valparaíso (PUCV)

Creador del Blog

Colaborador del Capítulo I

LOS SIETE PUENTES DE KÖNOGSBERG

Los Siete Puentes de Königsberg:

"El inicio de la Teoría de Grafos".

.

El llamado problema de "los siete puentes de Königsberg" fue lo que dio origen a la teoría de grafos.
Cabe señalar que Königsberg era Prusia oriental en el siglo XVIII y actualmente, Kaliningrado, provincia Rusa.

Durante mucho tiempo se intentó resolver el siguiente problema:


En la ciudad de Königsberg hay una isla y el río Pregel que la rodea se divide en dos brazos (como aparece en la imagen). La distintas zonas de tierra están unidos mediante siete puentes (color rojo). ¿Es posible dar un paseo por la ciudad, empezando por cualquiera de las cuatro partes de tierra firme, cruzando cada puente una y sólo una vez y volver nuevamente al punto de partida?

Después de un tiempo, en 1736, Leonhard Euler dio respuesta a este problema, dando origen a la teoría de grafos. Él representó por un punto cada sector de tierra y por una línea cada puente, uniendo los distintos puntos con tantas líneas como puentes haya entre dichos sectores, creando de esta forma, al primer grafo de la historia.


La representación de Euler fue similar a la siguiente imagen:

Euler se dio cuenta que la cantidad de líneas de cada punto tendría que ser par, para así poder entrar y salir de dicho punto, ocupando tan solo una vez cada puente.

En el problema de Königsberg, Euler demostró que era imposible recorrer la ciudad de la forma pedida, ya que el número de líneas que llegan a cada punto es impar y ésto implica que no es posible recorrerlos pasando una sola vez por cada uno de los puentes, es decir, no había solución paea ese problema.

KIRCHHOFF

Kirchhoff, en 1847, con el fin de estudiar el cálculo de la intensidad y la diferencia de potencial de cada elemento de la red, entre los cuales se encuentran: resistencias, bobinas, condensadores, fuente de tensión, etc., estudió los grafos conexos con el objetivo de desarrollar un método efectivo para el análisis de estas redes eléctricas.

Kirchhoff planteó que:

• La suma algebraica de las intensidades (corrientes) asociadas a los arcos incidentes a un vértice dado ha de ser 0 (No se acumula intensidad en ningún punto o nodo).
• La suma algebraica de los voltajes asociados a los arcos de cualquier ciclo ha de ser 0 (La diferencia de potencial ha de ser 0).

Imponiendo dichos postulados a cada uno de los nodos y ciclos del grafo que modela la red eléctrica se obtiene un sistema de ecuaciones lineales a resolver. El trabajo de Kirchhoff consistió en determinar un sistema equivalente y reducido de dichas ecuaciones. Se da lugar a un sistema de tantas ecuaciones lineales como elementos eléctricos hay.

Esquema de un Circuito Eléctrico Simple, que da origen a un Grafo.

CAYLEY

Cayley estudió el problema de la enumeración de los isomeros de los hidrocarburos saturados CnH2n+2 fijado el número n de átomos de carbono. Es decir se trataba de determinar el número de compuestos químicos con idéntica composición (fórmula) pero con distinta estructura molecular.

Para ello representó cada hidrocarburo mediante un árbol donde los vértices representaban los átomos (grado uno para los de hidrógeno y cuatro para los de carbono) y donde las aristas indicaban la existencia de enlaces químicos.

METANO - ETANO - PROPANO

TEOREMA DE LOS CUATRO COLORES

En 1852, Francis Guthrie plantea la siguiente conjetura: "En un plano no se necesitan más de cuatro colores para colorear un mapa de manera que dos regiones vecinas, es decir, que compartan una frontera y no únicamente un punto, no queden coloreadas del mismo color"

Este teorema tiene estrecha relación con la teoría de grafos.

Si los paises están distribuidos como se muestra en la imagen, bastaría sólo con dos colores.

Si se elige un punto para representar a cada país y se traza una línea uniendo dos puntos cada vez que correspondan a dos países adyacentes, se obtiene un grafo como el siguiente.

El problema del coloreado consiste en atribuir un color a cada vértice del grafo, de manera que dos vértices conectados tengan siempre un color diferente. Al distribuir los paises de la siguiente forma, ocuparemos sólo tres colores y obtenemos el siguiente grafo:

En el siguiente caso, necesitamos de 4 colores:

Este grafo es un K4 (completo de 4 vértices), que lo veremos más adelante

En 1976, K. Appel y W. Haken dan una prueba del teorema de los cuatro colores, demostrando mediante un programa computacional que, efectivamente, cuatro colores son suficientes para colorear cualquier mapa plano.

En 1996, N. Robertson, D. P. Sanders, P. Seymour y R. Thomas, publican una nueva prueba, sin los inconvenientes de la demostración de Appel y Haken, como el elevado número de configuraciones a estudiar y el tiempo que todo este procedimiento requiere.

Los grafos no sólo son importantes para los matemáticos. Se usan también para representar
circuitos electricos, además se pueden utilizar para determinar el trayecto óptimo (el menos costoso, el más rápido) de camiones que deben repartir y recoger productos a numerosos clientes, la red de carreteras puede modelizarse por un grafo, cuyas aristas son las carreteras de una ciudad a otra, a cada arista se le asocian varios números: longitud del camino correspondiente, tiempo de recorrido, peajes, etc. A través de grafo se pueden representar las lineas del metro, entre tantas otras aplicaciones.

DEFINICIÓN DE GRAFO

Un Grafo es un par (V(G), E(G)), donde:

• V(G) es un conjunto no vacío y finito de elementos {v1, v2, ……, vp}
• E(G) pertenece a V(G) x V(G) , o sea, define una relación R entre los vértices, puntos o elementos V(G).

El conjunto V(G) se denomina conjunto de vértices (puntos, nodos) y si vi y vj están en E(G), es equivalente a decir viRvj (vi, vj. están en V(G)) y esto se expresa diciendo que entre vi y vj existe una línea que se denota xij = (vi, vj) y E(G) se denomina el conjunto de líneas del grafo (o aristas). Los vértices v1 y v2 se denominan extremos de la línea.

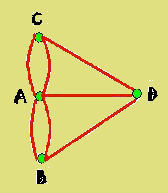
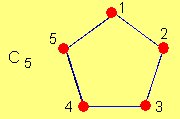
Ejemplo: El grafo representado a continuación, se obtiene a partir del conjunto de vértices

V={v1, v2,v3, v4, v5} y de la relación R es subconjunto de V x V, tal que, {(v1, v2)(v2, v3)(v4, v5)(v1, v4)(v2, v4) (v4, v4)(v2, v5)(v2, v3)} .

Una línea de la forma (u,u) la denominaremos lazo o bucle y una línea del tipo (u,v) con u distinto de v (uRv) la llamaremos línea simple. En cambio, cuando tengamos varias líneas que tengan como vértices terminales u y v, diremos que son líneas múltiples.

Observación: Las líneas (v2, v3) y (v3, v2) de la figura anterior son líneas múltiples y la línea (v4, v4) de la misma figura es un lazo.

En algunos casos es conveniente considerar grafos dirigidos en los cuales es necesario distinguir el sentido en que van las líneas, por medio de flechas.


Ejemplos:

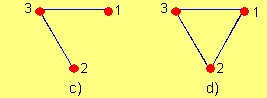
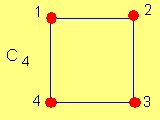
Este grafo se representa por:
G1 = (V(G1), E(G1))
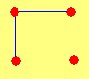
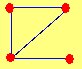
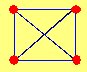
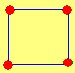
V(G1) = {1, 2, 3, 4}
E(G1) = {(1,2) (1,3) (1,4) (2,3) (2,4) (3,4)}

G1 es un grafo NO DIRIGIDO. Esto es que los pares de puntos (1,2) y (2,1) representan la misma línea. Es decir, si el vértice 1 está conectado con el vértice 2, entonces el vértice 2 está conectado con el vértice 1.


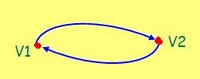
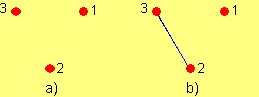
Ahora bien, si tenemos el siguiente grafo:

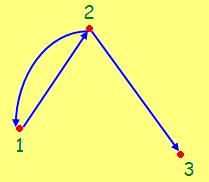
Este grafo, sin embargo, se representa por:
G2 = (V(G2), E(G2))
V(G2) = (1,2,3)
E(G2) = ( (1,2) (2,1) (2,3) )

Aquí se repiten las conexiones de 1 con 2 porque este, como se ve, es un grafo DIRIGIDO. En este tipo de grafos si 1 está conectado con 2, no necesariamente 2 está conectado con 1.

Esto es lo que la mayoría de los autores denominan multigrafo. Sin embargo, nos dedicaremos a estudiar un tipo particular de grafos denominados grafos simples o matemáticos, que son aquellos grafos que no poseen orientación, ni líneas múltiples, ni lazos.

Usaremos la notación utilizada por F. Harary, denotaremos la cardinalidad del conjunto de vértices de un grafo simple como V(G)= p y la cardinalidad del conjunto de líneas del grafo como E(G) = q.

GRAFOS: RELACIÓN DE EQUIVALENCIA

Si la relación es reflexiva, significa que por ejemplo v1Rv1, lo que indica que el vértice v1 tiene un lazo.

Si en un grafo dirigido la relación R es simétrica, es decir, v1Rv2 entonces v2R v1, tenemos que existen dos líneas que unen a v1 y v2.

Si la relación es transitiva, o sea, (v1Rv2) y (v2Rv3) si y sólo si v1Rv3, se tiene la existencia de un triángulo v1 v2 v3.

Grado o valencia de un vértice (se denota grad(vi) o val(vi)) e indica el número total de líneas que tiene un vértice vi.
En el problema de los puentes de Königsberg (resuelto por Euler) encontramos un multigrafo de cuatro vértices y siete líneas que representan la relación entre los vértices.
Los vértices A, B, D tienen tres líneas y el vértice C cinco líneas. De este modo, tenemos

val(A) = val(B) = val(D) = 3 y val(C) = 5.

Si tenemos una línea xij = (vi, vj), entonces los vértices vi y vj se llaman vértices adyacentes y a vi lo denominaremos vértice inicial y vj vértice final. Además se dice que la línea es incidente al vértice vi como también es incidente al vj.
Las líneas son concurrentes entre sí, si varias líneas tienen un vértice vi en común.

Las líneas (A, C), (C, D), (B, C) son concurrentes entre sí. Entonces el número total de líneas concurrentes al vértice vi es igual al grado o valencia de vi.
A los vértices con valencia mínima los denotaremos con d(G) y aquellos vértices con valencia máxima D(G).

En el grafo anterior vemos que d(G) = 3 y D(G) = 5.


En particular, si d(G) = D(G) = r, entonces todos los vértices de G tienen la misma valencia "r" y el grafo se dice regular de grado r.

Obs.: No siempre es posible construir grafos regulares para valores cualesquiera de p, q y r, ya que de acuerdo con el Teorema de Euler se debe cumplir con 2q = pr.


Al conjunto de todos los vecinos de un vértice dado le llamaremos vecindad de vi o conjunto de adyacencia de vi, y se denota N(vi).
Así, N(vi) = { vj/ vjRvi }.

En particular, un vértice vi para el cual N(vi)= 0, se le denomina vértice aislado.

Por ejemplo, en el siguiente grafo v4 es un punto aislado.

TEOREMA DE LAS VALENCIAS

La suma de las valencias de los vértices de un grafo es dos veces el número de líneas, es decir, si G es un grafo con "p" vértices y "q" líneas, entonces val(v1) + val(v2) + ... + val(vp) = 2q.

Demostración: Si vi pertenece a N(vj), entonces vj pertenece a N(vi), lo que implica que la línea (vi, vj) es contada dos veces. Como esto ocurre para cada vértice vi, con i entre 1 y p, la suma de todos los vi es 2q.

Corolario: En todo grafo G el número de vértices con valencia impar debe ser par.

Demostración: Los vi que pertenecen a V(G), con val(vi') par y los vi'' con val(vi'') impar.

Luego, .

Pero, la es par y 2q es un número par, lo que implica que la es la diferencia de dos números pares, y por lo tanto es par.

Lo anterior es muy útil para verificar la existencia de grafos.
Por ejemplo, si tenemos los siguientes datos:
El grafo tiene 5 puntos, donde:
Val (1) = 2
Val (2) = 3
Val (3) = 1
Val (4) = 1
Val (5) = 4
Entonces no existe grafo alguno que cumpla con esta condición, pues viola el teorema anterior, ya que existen 3 puntos con valencia impar, y como vimos en la demostración la cantidad de vértices con valencia impar, debe ser par.

TEOREMA: Sea un grafo G = (p,q); entonces:

a) Si "p" es par, existen grafos regulares de cualquier valencia r, si .
b) Si "p" es impar, existen grafos regulares solamente de valencia par r y si .

Por ejemplo, si p = 7 existen grafos regulares de grado 2, 4 y 6

ISOMORFISMO DE GRAFOS

Definición:

Se dirá que dos grafos G y G' son isomorfos entre sí, si:

• Existe una función biyectiva .
• Si dos vértices vi, vj son adyacentes en V(G), es decir, viRvj, entonces las correspondientes imágenes de dichos vértices también son adyacentes pero en V(G'), dicho de otra forma, ; y viceversa.
  
  
  Ejemplo: En la siguiente figura, tenemos que G es isomorfo a G'.

Donde V(G) = {1,2,3,4} y V(G') = {A,B,C,D} y como debe cumplirse que f:V(G) V(G') es una biyección, entonces f(1) = D, f(2) = B, f(3) = C, f(4) = A. Observar que 1R4 en G, entonces, D R A en G'.

Tenemos otra función que también define un isomorfismo entre G y G'.
f(1) = B, f(2) = D, f(3) = C y f(4) = A.
Observar, igualmente, que para este caso 1 R 4 en G, entonces, B R A en G'.

La relación de isomorfismo preserva las vecindades de cada vértice.

La relación de isomorfismo de dos grafos G y G' se denota de la siguiente manera,

Corolario: Si , entonces:

1. /V(G) /= /V(G')/
2. /E(G) /= /E(G') /
3. Si tiene vi tiene "k" vértices vecinos vi1, vi2, vi3, ... , vik, entonces, f(vi) tiene los siguientes "k" vértices vecinos f(vi1), f(vi2), f(vi3), ... , f(vik).
4. vi y f(vi) tienen la misma valencia.
   

CARACTERIZACIÓN DE LOS GRAFOS

Un problema interesante en la teoría de grafos, que no ha sido resuelto del todo, es el referente a la búsqueda de todos los grafos simples diferentes que existen con un número determinado de vértices (caracterización de los grafos). Así, para p = 1 hay un solo grafo.

Así, para p = 1 hay un solo grafo.

Para p = 2, existen dos grafos diferentes.

Para p = 3 ya llegan a ser cuatro grafos

.

Pero para p = 4 ya nos encontramos con once grafos distintos.

Si hacemos esto para todos los grafos simples diferentes que existen con un número "p" de vértices, vemos que a medida que "p" crece el número de grafos aumenta considerablemente.

Esto es un problema muy complejo, y para que se tenga una idea, cuando p = 9, existen 274668 grafos diferentes y conviene clasificar los grafos en ciertas familias de acuerdo a algunas propiedades específicas.

• Grafos Nulos (Np), son aquellos grafos que presentan solamente vértices aislados y por lo tanto, no existe una relación R entre sus vértices, es decir, /V(G)/= p y /E(G)/= 0.
• Grafos Completos (Kp), son grafos donde cada vértice está relacionado con todos los (p-1) vértices restantes.

Si tengo "p" vértices hay p (p-1) posibles líneas. pero como el grafo es simple, cada línea se cuenta dos veces. Luego hay un total de p(p-1)/2 líneas.

Esntonces /V(Kp)/= p y /E(Kp)/= p(p -1)/2

Algunos ejemplos de los cinco primeros Kp

Por ejemplo, la familia de los Grafos Nulos (Np), considera aquellos grafos que presentan solo vértices aislados y por lo tanto, no existe una relación R entre sus vértices, es decir, /V(G)/= p y /E(G)/= 0.

En contraposición, existe la familia de los Grafos Completos (Kp), donde cada vértice está relacionado con todos los (p-1) vértices restantes. Ahora, si tengo "p" vértices hay p(p-1) posibles líneas. Sin embargo, el grafo es simple y cada línea se cuenta dos veces, luego, hay un total de p(p -1)/2 líneas, o sea, /V(Kp)/= p y /E(Kp)/= p(p-1)/2 .

Otra familia de particular interés son los llamados Ciclos, que denotaremos Cp , donde "p" es el número de vértices. Son grafos regulares de valencia 2, donde el número de líneas q = p. También son conocidos (sobre todo en geometría) como los "p-ágonos". Algunos de los grafos que forman esta familia son los siguientes:

Triángulo ------>

Cuadrado ------>

Pentágono ---->