GRAFOS EULERIANOS Y HAMILTONIANOS

Existen todavía algunas familias de grafos que se derivan del concepto de grafos conexos. Este es el caso de los grafos eulerianos y los grafos hamiltonianos. Estas familias de grafos nos permiten resolver el famoso problema de los puentes de Königsberg:
¿cuándo es posible hacer un recorrido de una figura (en este caso de un grafo múltiple) sin pasar dos veces por la misma línea o por el mismo vértice?

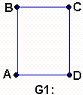
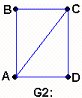
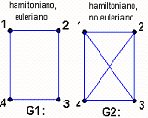
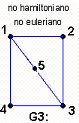
En la fig. 3.10 tenemos dos grafos G1 y G2; es posible recorrer uno de ellos sin repetir ninguna línea, pero el otro no. ¿Cuál es cuál? Es evidente que el grafo G1 no puede ser recorrido sin repetir alguna de sus líneas, mientras que el grafo G2 sí.

Fig 3.10

I. GRAFOS EULERIANOS

Recorrido cerrado

Cubre todas las líneas de un grafo, comenzando y terminando en un mismo vértice, recorriendo sin repetición y en forma continua todas las líneas de un grafo G cualquiera. Cuando tal recorrido existe, se denomina euleriano y un grafo que se puede trazar mediante un recorrido euleriano se llama grafo euleriano. En la fig. 3.11, G1 es obviamente un grafo euleriano; G2 no lo es, a pesar de que se puede trazar continuamente, ya que el recorrido comienza y termina en vértices distintos; finalmente, G3 no es un grafo euleriano, porque no se puede trazar continuamente.

Fig. 3.11

Teorema 3.2

Diremos que un grafo G es la unión disjunta de ciclos, si podemos descomponer a G como la unión de ciclos que no tienen líneas en común, aunque se permite que tengan, al menos, un vértice en común.

Fig. 3.12

En la fig. 3.12, el grafo se puede descomponer como la unión disjunta de los ciclos C = v1v2v3v4v5v6v1; C' = v1v7v5v1; C'' = v2v7v4v2; C''' = v3v8v9v3 y el recorrido euleriano para el grafo G viene dado por la secuencia de sus líneas 1, 2,..., 15.

OBSERVACION 3.1.5: Esta descomposición por lo general no es única. El grafo de la fig. 3.11 admite otra descomposición como unión disjunta de ciclos, por ejemplo, C = v1v2v7v1; C' = v3v4v2v3; C'' = v3v8v9v3; C''' = v7v4v5v7; C'''' = v5v1v6v5 .

TEOREMA 3.2

Un grafo G conexo es euleriano si y sólo si es la unión disjunta de ciclos.

Demostración:
Si G es euleriano, G admite un recorrido euleriano T. Como T es cerrado, T contiene un ciclo C. Sea T' el recorrido obtenido al eliminar en T las líneas de C. T' sigue siendo un recorrido cerrado, por lo tanto, contiene un ciclo C'. Repitiendo este proceso, obtenemos una descomposición de G como la unión disjunta de los ciclos C, C'..., etc.

Recíprocamente, supongamos que G es una unión disjunta de ciclos. Sea C un ciclo cualquiera en G. Si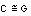

entonces G es un ciclo y por lo tanto euleriano. Si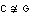

existe un ciclo C' en G que tiene un vértice v en común con C (por hipótesis). Si G es la unión de C y C', entonces, comenzando en v trazamos C y luego C', obteniendo así un recorrido euleriano de G. Si la unión de C y C' no es todo G, existe un ciclo C'' que tiene algún vértice v' en común con C o con C', digamos por ejemplo con C'. Si G es la unión de C, C' y C'', entonces comenzando en v trazamos C, luego trazamos C' hasta llegar a v' y luego trazamos C'' hasta completar C', luego regresamos a v como ilustra el diagrama de la fig. 3.13.

Fig. 3.13

Así, obtenemos un recorrido euleriano de G. Si la unión de C, C' y C'' no es todo G, continuamos con este procedimiento hasta obtener un recorrido euleriano de G.

COROLARIO 2: Un grafo conexo es euleriano si y sólo si todos sus vértices tienen valencia par. (Este teorema rige también para multigrafos).

Demostración:
En un recorrido euleriano, cuando visitamos un vértice, necesitamos al menos dos líneas distintas adyacentes al vértice (una para llegar al vértice y otra para salir de él), incluyendo al vértice inicial, porque tenemos que regresar a él para concluir el recorrido. Esto significa, que cada vértice contribuye con un número par de líneas y, por lo tanto, su valencia es par.



II. GRAFOS HAMILTONIANOS

¿Cuándo es posible hacer un recorrido en un grafo que pase por cada vértice exactamente una vez y termine en el vértice original?
O en otras palabras, ¿cuándo un grafo tiene un ciclo cerrado que contenga a todos sus vértices?

Cuando existe tal ciclo, lo llamaremos ciclo hamiltoniano y un grafo que posea un ciclo hamiltoniano se llama grafo hamiltoniano.

Un ciclo puro Cp es evidentemente hamiltoniano; el grafo de la fig. 3.14 también. En efecto, el ciclo v1v2... v7v1 representa un ciclo hamiltoniano del grafo G.

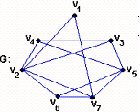
Fig. 3.14

La Fig. 3.15 muestra que no hay ninguna relación directa entre grafos eulerianos y hamiltonianos.

Fig. 3.15

Contrario al caso de los grafos eulerianos, para el caso de los grafos hamiltonianos no se conoce ninguna condición necesaria y suficiente que los caracterice. Esto es lamentable porque en muchas aplicaciones es fundamental poder determinar si un grafo es hamiltoniano.

¿Qué tan fuertemente conexo es un grafo?

Una posible interpretación de esta pregunta es analizar cuántas líneas o vértices deberíamos eliminar del grafo para convertirlo en no conexo. Introducimos a continuación algunas definiciones que aclaran este punto.

III. PUNTOS DE CORTE Y PUENTES

Sea G un grafo conexo. Un vértice en G se llama un punto de corte de G si G - vi no es conexo. Un punto de corte de un grafo G no conexo es un punto de corte de alguna de sus componentes.

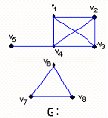
Ahora bien, sea G un grafo conexo. Una línea de G se llama puente de G si el grafo obtenido al eliminar xj no es conexo. Si G es un grafo no conexo, decimos que xj es un puente de G, si es un puente de una de las componentes de G. Ilustremos estos dos conceptos en la fig. 3.16.

Ejemplo 9:

Fig. 3.16

- v4 y v6 son puntos de corte del grafo G. En este caso, éstos son los
únicos.
- G tiene dos puentes, (v4, v5) y (v4, v6).

A veces un grafo no tiene puntos de corte, por ejemplo el grafo Kn . Otras veces puede tener muchos puntos de corte, por ejemplo un camino Pn con n mayor o igual a 3 que une dos vértices v, w como en la fig. 3.17. En este caso todo vértice, excepto v y w, es punto de corte.

Fig. 3.17

El siguiente teorema nos dice que este último ejemplo corresponde a un grafo con un número muy elevado de puntos de corte, a saber (n - 2) si el camino tiene n vértices; ya que, todo grafo G conexo tiene que tener por lo menos dos vértices que no son puntos de corte.

TEOREMA 3.3

Todo grafo G conexo con más de un vértice tiene por lo menos dos vértices que no son puntos de corte.

Demostración: (por inducción en el número de vértices)

Sea n el número de vértices del grafo G y Pn la proposición: Todo grafo conexo con más de dos vértices tiene por lo menos dos vértices que no son puntos de corte.

En este caso nuestro punto de partida para la inducción es n = 2, luego P2 es verdadera, ya que el único grafo G conexo con dos vértices es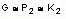

y ninguno de los dos vértices es punto de corte.
Supongamos que todo grafo G conexo con menos de n vértices (n > 2) tiene por lo menos dos vértices que no son puntos de corte (hipótesis inductiva).
Veamos que también se cumple para un grafo G conexo con n vértices. Se presentan dos casos:

CASO I.

G no tiene puntos de corte. Si G no tiene puntos de corte, entonces el teorema se cumple automáticamente, ya que el grafo (en este caso) tiene n vértices con n > 2 que no son puntos de corte.

CASO II.

G tiene, por lo menos, un punto v de corte. Si eliminamos este punto de corte v, el grafo G - v está formado por las componentes conexas G1, G2,..., Gt de G - v. Ahora, el grafo G - v tiene (n - 1) vértices y por lo tanto, se cumple la hipótesis inductiva, es decir, G - v tiene por lo menos dos puntos que no son de corte. Sin embargo, siguen existiendo dos posibilidades:

Caso II.1.

Que para todo Gi= vi, con i entre 1 y t, entonces G sería una estrella K1,i , o sea, tendría la forma de la fig. 3.17. En este caso, ninguno de los vértices vi, con i entre 1 y t, es un punto de corte, y por lo tanto, el teorema se cumple.

Fig. 3.18

Caso II.2.

Que alguna de las componentes Gi, con i entre 1 y t, tiene más de dos vértices. Sin perder generalidad, podemos decir que G1 tiene más de un vértice. Por la hipótesis inductiva, G1 tiene dos vértices que no son puntos de corte de G1, digamos vi y vj.


- Caso II.2.1.

Si ambos vértices vi y vj son adyacentes a v, como lo muestra la fig. 3.18, vi y vj no pueden ser puntos de corte de G, porque al eliminar cualquiera de ellos no se desconecta el grafo.

Fig. 3.19

- CASO II.2.2.

Si uno de los dos vértices, digamos vi , no es adyacente a v en G, no puede ser punto de corte de G, como lo muestra la fig. 3.19. Por lo tanto, cada componente Gi, con i entre 1 y t, tiene por lo menos un punto de corte de G. Luego, existen a lo sumo t puntos de corte en G, entonces, como t está entre 2 y n, hay (n - t) puntos que no son de corte. Luego, Pn es verdadera.

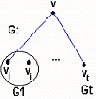
Fig. 3.20

TEOREMA 3.4

v es un punto de corte en un grafo conexo G, si y sólo si existen vértices u y w, ambos distintos de v, tales que todo camino que une a u con w pasa por v.

Demostración:

Si v es punto de corte de G, G - v tiene por lo menos dos componentes G1, G2. Si elegimos un vértice u en G1 y un vértice w en G2, no hay camino alguno que una a u con w en G - v, pero sí los hay en G, porque G es conexo.
Recíprocamente, si existen u y w distintos de v, tales que todo camino que una a u con w pasa por v, G - v tiene que ser no conexo.



TEOREMA 3.5

En un grafo conexo G una línea x es un puente de G si y sólo si existen vértices u y w tales que todo camino que una a u con w contiene a x.

Demostración:

Si x es un puente de G, G - x tiene por lo menos dos componentes conexas G1 y G2 (por definición de puente). Tomando un vértice u perteneciente a G1 y un vértice w perteneciente a G2, no existe un camino que una a u con w en G - x, pero sí lo hay en G, porque G es conexo. Por lo tanto, todos los caminos que unan a u con w deben pasar por x.
Recíprocamente, si existen vértices u y w en G, no incidentes a x, tales que todo camino que una a u con w pase por x, entonces G - x tiene que ser no conexo.
Podemos resumir los teoremas anteriormente vistos en los siguientes dos teoremas generales.

TEOREMA 3.6

Sea v un vértice cualquiera de un grafo conexo G; entonces los siguientes enunciados son equivalentes:

(1) v es un punto de corte de G.
(2) Existen vértices u y w, diferentes de u, tales que v está en todo camino que va de u a w.
(3) Existe una partición del conjunto de vértices V - {v} en subconjuntos U y W, tales que, para cualquier par de vértices u perteneciente a U y w perteneciente a W, el vértice v está en todo camino (u, w).

TEOREMA 3.7

Sea x una línea cualquiera de un grafo conexo G; entonces los siguientes enunciados son equivalentes:
(1) x es un puente de G.
(2) x no se encuentra en ciclo alguno de G (en caso de que G tenga ciclos).
(3) Existen vértices u y v del grafo G tales que la línea x está en cada camino que una a u con v.
(4) Existe una partición del conjunto de vértices V en dos subconjuntos U y W, tales que para cualquier par de vértices u perteneciente a U y w perteneciente a W, la línea x está en todo camino que una a u y w.


IV. BLOQUES

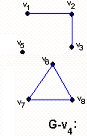
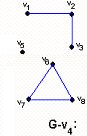
Una consecuencia inmediata del Teorema 3.5 es que, con la excepción de K2, en un grafo conexo todo puente es incidente con un punto de corte y por lo tanto todo grafo conexo, excepto K2, que contiene un puente, contiene puntos de corte. El recíproco de esta proposición no se cumple, como se puede ver en el ejemplo de la fig. 3.20 (G contiene, al punto de corte v, pero no contiene puentes).
Es fácil ver que, si una línea pertenece a un ciclo de G, dicha línea no puede ser un puente. Recíprocamente, si la línea x = ( vi, vj ) no pertenece a ciclo alguno de G, entonces para los vértices vi y vj y el único camino que los une consiste de la línea x; y por lo tanto se cumple, trivialmente, que todo camino que una a vi con vj contiene a x. Por el Teorema 3.5, x es un puente.

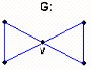
Fig. 3.21

Con lo expuesto anteriormente queda demostrado el siguiente teorema:

TEOREMA 3.8

Una línea x es un puente en un grafo conexo G si y sólo si x no pertenece a ciclo alguno de G.

Hemos visto que existen grafos que no contienen puntos de corte ( Kn por ejemplo). Un grafo conexo con más de un vértice que no contiene puntos de corte se llama bloque.

OBSERVACION 3.1.6:

Para p = 2, el único bloque que existe es K2 . Este es un caso especial porque, aunque no tiene puntos de corte, tiene un puente. En todos los demás casos un bloque no puede contener puentes. Como ya habíamos mencionado, la existencia de un puente implica, excepto en el caso de K2, la existencia de puntos de corte.

El siguiente teorema nos da una caracterización de bloques para grafos con más de dos vértices.

TEOREMA 3.9

Un grafo G con p mayor o igual a 3 es un bloque si y sólo si cada par de vértices de G pertenece a algún ciclo en G.

Demostración:

Supongamos que G es tal que cada par de vértices pertenece a algún ciclo común en G. Evidentemente G es conexo. Si G no fuera un bloque, G tendría un punto de corte v y por el Teorema 3.4 deberían existir dos vértices, vi y vj, tales que todo camino que una a vi con vj contiene a v. Pero por hipótesis, vi y vj están en algún ciclo de G y por lo tanto hay dos caminos entre y que no tiene vértice alguno en común. Evidentemente, v no puede pertenecer a ambos caminos, y por lo tanto, si eliminamos v, no se desconecta el grafo G. Luego, v no puede ser punto de corte (ver fig. 3.22).
Recíprocamente, supongamos que G es un bloque con p mayor o igual a 3, y sean vi y vj dos vértices cualesquiera en G. Como G es conexo, debe existir por lo menos un camino que una a con . Además, si hubiera uno solo, cada una de las líneas de ese camino sería un puente (por el Teorema 3.5) y como G es un bloque, él no tiene puentes y esto no puede ocurrir. Por lo tanto deben existir por lo menos dos caminos distintos que unan a vi con vj. Como G no tiene puntos de corte, los caminos no pueden tener un vértice v en común, ya que, por el Teorema 3.4, v sería un punto de corte (ver fig. 3.23).

Fig. 3.22

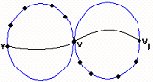
Fig. 3.23

Por lo tanto, debemos tener dos caminos que no tengan vértices en común, como en la fig. 3.24, lo cual inmediatamente nos daría un ciclo

Fig. 3.24

o debería haber tres caminos tales que cada dos de ellos tienen un vértice distinto en común (ver fig. 3.25).

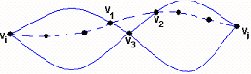
Fig. 3.25

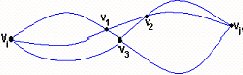
Fig. 3.26

Pero en este caso, como lo indica la fig. 3.26, también tenemos un ciclo que contiene a vi y vj.

El siguiente teorema resume los resultados anteriormente vistos y otros aspectos importantes acerca de los bloques.

TEOREMA 3.10

Sea G un grafo conexo con al menos tres vértices; entonces los siguientes enunciados son equivalentes:

(1) G es un bloque.
(2) Cada dos vértices cualesquiera de G están en un ciclo común.
(3) Cada vértice o línea de G está en un mismo ciclo.
(4) Cada dos líneas de G están en un ciclo común.
(5) Dados dos vértices cualesquiera de G y una línea también de G,
existe un camino que une los vértices y que además contiene la línea que pertenece a G.
(6) Para cualesquiera tres vértices distintos de G existe un camino que une a dos de ellos y que contiene al tercero.
(7) Para cualesquiera tres vértices distintos de G, existe un camino que une
dos de ellos, pero que no contiene al tercero.