GRAFOS N-CONEXOS

El concepto de conexión dentro de un grafo G es particularmente intuitivo y generaliza los conceptos de punto de corte, puente y bloque. Para los cuatro grafos dados en la fig. 3.27 podemos observar que G1 es el que tiene la propiedad mínima de ser conexo, ya que con simplemente eliminar una línea cualquiera, desconectamos el grafo. No puede G2 ser desconectado por la simple eliminación de una línea, pero sí por la eliminación de un vértice, el punto de corte. Por otra parte, podemos ver que no hay puntos de corte ni puentes en G3, pero es claro que no es tan fuertemente conexo como

Fig. 3.27

Por lo dicho anteriormente nos resultará útil considerar cuando los vértices o las líneas de un grafo G pueden desconectarlo, sin que sean puntos de corte ni puentes, ya que estos casos son triviales. Mientras más líneas haya que eliminar para que un grafo deje de ser conexo, se habla de la capacidad que tiene el grafo de ser conexo. Para ello definamos los siguientes dos parámetros.


I. CONEXION PUNTUAL (G) Y CONEXION LINEAL (G)

La conexión puntual, k(G), es el número mínimo de vértices que al ser eliminados dan como resultado un grafo no conexo ó K1 (trivial). Así, por ejemplo, la conexión puntual de un grafo no conexo es cero, k(G) = 0; mientras que K(G), con G conexo, que tenga un solo punto de corte, es uno: k(G) = 1. Por otra parte, Kp es el grafo más fuertemente conexo que existe, para el cual k(kp ) = (p -1).

La conexión lineal, k(G), es el menor número de líneas que al ser eliminadas, desconectan al grafo o lo convierten en un grafo trivial. Análogamente, la conexión lineal para un grafo no conexo es cero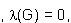

mientras que si el grafo es conexo y posee un puente, entonces (G) = 1.

Existe una desigualdad entre

descubierta por Whitney (1932) y que enunciaremos en el siguiente teorema.


TEOREMA 3.11

Para todo grafo G conexo, se cumple que
Demostración:

Sea G un grafo conexo trivial, o sea un k1; entonces claramente G no tiene líneas, luego

Sea ahora G un grafo conexo no trivial y sea v un vértice de G con valencia mínima, es decir, val(v) = (G). Entonces, el conjunto de las líneas incidentes al vértice v, al ser eliminadas desconectan al grafo, es decir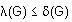

Probaremos que utilizando inducción sobre

entonces G debe ser el grafo trivial o un grafo no conexo. En ambos casos

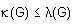Análogamente si Supongamos quepara todos los grafos G que tengan una conexión lineal (hipótesis inductiva). Consideremos ahora un grafo G con y sea x una línea en el conjunto de las n líneas que al ser eliminadas desconectan al grafo. Sea H el grafo resultante de eliminar de G la línea x, entonces, (por la hipótesis inductiva) y por lo tanto, se cumpleAhora bien, G tiene una línea más que H, y esta línea no es un puente porque si lo fuera Entonces, si para Hpara G, 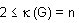ya que al no ser esta línea un puente, los vértices de la línea no desconectan al grafo.

OBSERVACION 3.3.1:

Las desigualdades del Teorema 3.11 son con frecuencia estrictas. Así, el grafo de la fig. 3.28 tiene

Fig. 3.28

Esta observación puede ser generalizada para construir grafos que tengansiendo a, b, c números enteros positivos que cumplan con

CASO I. Si a = b = c, entonces .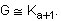
CASO II. Si a< b =" c," style="DISPLAY: block; MARGIN: 0px auto 10px; CURSOR: hand; TEXT-ALIGN: center" alt="" src="http://photos1.blogger.com/x/blogger/6690/3990/320/162804/66.jpg" border="0"> CASO III. Si b< style="DISPLAY: block; MARGIN: 0px auto 10px; CURSOR: hand; TEXT-ALIGN: center" alt="" src="http://photos1.blogger.com/x/blogger/6690/3990/320/249915/67.jpg" border="0">

Fig. 3.29

TEOREMA 3.12

Entre todos los grafos con p vértices y q líneas, la máxima capacidad de ser conexo es cero, cuando q < style="DISPLAY: block; MARGIN: 0px auto 10px; CURSOR: hand; TEXT-ALIGN: center" alt="" src="http://photos1.blogger.com/x/blogger/6690/3990/320/733004/68.jpg" border="0"> , cuando Demostración:

Si q<>k(G) = 0, ya que al ser el número de líneas menor que el número de vértices menos 1, el grafo es no conexo.

Si entonces ya que hay que recordar que la suma de las valencias de los vértices del grafo G es igual a 2q, y el promedio de las valencias es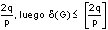

pero sabemos por el Teorema 3.11 que

La valencia promedio es

Veamos el ejemplo de la fig. 3.30.

Ejemplo 10:

Fig. 3.30

por otra parte, la valencia promedio



Sin embargo, debemos aclarar la nueva notación introducida a propósito de la demostración del Teorema 3.12. Dado un grafo cualquiera G = (p, q), tenemos pares de enteros (p, q) donde p es el número de vértices y q el número de líneas y donde además (p - 1, q) ó (p, q - 1) no desconectan al grafo G.


COROLARIO 3: La máxima conexión lineal de un grafo (p, q) cualquiera es igual a la máxima conexión puntual.

OBSERVACION 3.3.2: Recientemente se ha estudiado la posibilidad de separar un grafo G mediante la eliminación mixta de vértices y líneas. Se llama conexión par de un grafo G cualquiera, G = (p, q), al par ordenado (a, b) de números enteros no negativos, tales que existe un número a de vértices y b de líneas cuya eliminación desconecta al grafo G y además no existen los pares ordenados (a -1, b) ó (a, b -1) con esta propiedad. Así, en particular,
son conexiones pares de G, ya que son una generalización de los conceptos de conexión puntual y lineal. Se ha visto que para todo valor de a, comprendido entre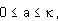

existe una única conexión par (a, b), de este modo G tiene exactamente k+1 conexiones pares.

Se dice que un grafo G es n - conexo si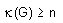

y es n - linealmente conexo si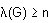Podemos observar que un grafo G no trivial es 1 - conexo si y sólo si G es conexo, y es 2 - conexo si y sólo si es un bloque que tiene más de una línea, por lo tanto 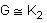es el único bloque que no es 2 - conexo.

Para estudiar aplicaciones relacionadas con la propiedad de un grafo de ser n - conexo, necesitamos conocer el número máximo de caminos que pasan por dos vértices, u y w de G, en los casos en los cuales:
a) los caminos no comparten líneas en común; estos caminos los llamaremos caminos disjuntos por líneas y
b) caminos que solamente tienen en común los vértices u y w; estos caminos los llamaremos caminos disjuntos por vértices.

En la fig. 3.30 vemos claramente que hay solamente tres caminos disjuntos por líneas y dos caminos disjuntos por vértices entre v y w.

Para ilustrar por medio de un ejemplo la definición de caminos disjuntos por líneas, podemos considerar las siguientes secuencias: (1) v, a, d, f, w; (2) v, b, e, h, w; (3) v, c, e, i, w. En el caso de los caminos disjuntos por vértices, podemos considerar: (1) v, a, d, f, w y (2) v, c, e, i, w. En cambio, si consideramos los vértices b y w, vemos que existen cuatro caminos disjuntos por líneas y dos caminos disjuntos por vértices.

Los grafos n - conexos poseen una aplicación práctica en la distribución de fluidos. Consideremos, por ejemplo, en la fig. 3.31 que el vértice v sea un pozo de petróleo y w el tanque de almacenamiento; los caminos vendrían siendo las diferentes rutas de distribución del fluido para las diferentes ciudades. Si b fuera el pozo y w el tanque, también podríamos distribuir el petróleo por todos los vértices del grafo, que consideraremos ciudades, sin pasar dos veces por una misma ciudad.

TEOREMA 3.14 (Whitney)

Un grafo G con p mayor o igual a 3 es 2 - conexo si y sólo si dos vértices cualesquiera de G están conectados al menos por dos caminos disjuntos.

Demostración:

Si dos vértices cualesquiera, u y v, de G están conectados por al menos dos caminos disjuntos por líneas, entonces claramente G es conexo y no tiene puntos de corte, luego G es 2 - conexo.
Recíprocamente, sea G un grafo 2 - conexo. Demostraremos por inducción aplicada a la distancia d(u, v) entre dos vértices cualesquiera u, v pertenecientes a G, que ellos están siempre conectados por al menos dos caminos disjuntos por líneas.
Supongamos que d(u, v) = 1. Luego, como G es 2 - conexo, la línea (u, v) no es un puente y por lo tanto está contenido en un ciclo (por el Teorema 3.8), es decir, u y v están conectados por dos caminos disjuntos por líneas en G. Consideremos que se cumple para dos vértices cualesquiera u y v que están a distancia menor que n y sea ahora d(u, v) = n, con n mayor o igual a 2. Sea un camino (u, v) cualquiera de longitud n y sea w un vértice de G que precede a v en el camino, entonces d(u, v) = n - 1 y por lo tanto, por la hipótesis inductiva, existen dos caminos (u, w) disjuntos que llamaremos P y Q (ver fig. 3.32).

Fig. 3.32

Como G es 2 - conexo, G - w es conexo, luego debe existir un camino P' en G que una a u con v (ver fig. 3.33).

Fig. 3.33

Sea t el último vértice de P' que también está en P unión Q (ver fig. 3.33) porque está en P. Entonces, G tiene dos caminos (u, v) disjuntos por líneas, a saber, P' y el camino (por ejemplo) Q con (w, v).

COROLARIO 4: Si G es 2 - conexo, entonces cualesquiera dos vértices de G están en un mismo ciclo.

Con la finalidad de generalizar el Teorema 3.14, es conveniente introducir la operación de subdivisión de una línea. Una línea x se dice que se subdivide cuando se reemplaza por un camino de longitud dos. Esta definición se muestra en la fig. 3.34.

Fig. 3.34

OBSERVACION 3.3.3: Es evidente que la operación de subdivisión es cerrada en el conjunto de grafos bloques, siempre y cuando dichos bloques contengan al menos tres vértices, ya que si al bloque k2 le aplicamos la operación de subdivisión, obtenemos un P3 que no es bloque.

COROLARIO 5: Si G es un bloque con p mayor o igual a 3, entonces dos líneas de G pertenecen a un mismo ciclo.

Existe una caracterización del Corolario 5 para grafos 3 - conexos, pero antes debemos introducir el concepto de grafo rueda, descubierto por un eminente grafista llamado W. T. Tutte. Para p mayor o igual a 4, la rueda Wp está definida como (ver fig. 3.35).

Fig. 3.35

TEOREMA 3.15 (Tutte)

Un grafo G es 3 - conexo, si G es una rueda o se puede obtener a partir de una rueda mediante una sucesión de operaciones del siguiente tipo:
1) Agregar una nueva línea.
2) Reemplazar un vértice v que tenga valencia a lo menos cuatro, por dos vértices adyacentes v' y v'', tal que, cada vértice formalmente unido con v se una exactamente con v' o v''. De modo que en el grafo resultante la valencia de v' será mayor o igual que tres al igual que la valencia de v'' .

OBSERVACION 3.3.4: Cuando se efectúan operaciones sobre el grafo

siempre se aumenta su conexión puntual.

La conexión puntual para la ruedaWp , con p mayor o igual a 4, es Sin embargo, la eliminación de los vértices no puede ser al azar; debemos eliminar el vértice del centro y cualesquiera dos o más de los vértices de afuera que no sean adyacentes entre sí.

Ejemplo 11: El grafo G de la fig. 3.36 es 3 - conexo, ya que se puede obtener de la rueda .

Fig. 3.36

Pero también podemos determinar si un grafo cualquiera G es 3 - conexo, convirtiéndolo en una rueda.
Ejemplo 12: Sea el grafo G de la fig. 3.37, lo llevaremos a una rueda para demostrar que es 3 - conexo. Después de efectuar varias operaciones, nos queda una rueda W5, luego el grafo G es 3 - conexo.

Fig. 3.37

Una n - componente de un grafo G es el máximo subgrafo n - conexo. En particular, las 1 - componentes de G son las componentes no triviales de G, mientras que las 2 - componentes son los bloques de G con al menos 3 vértices, (Harary y Kodama [HK1] en el año 1964).

Ejemplo 13: Un grafo G con dos 3 - componentes que tienen dos vértices en común se muestra en la fig. 3.38.

Fig. 3.38

Todos estos resultados conducen a un teorema descubierto por Mengen en 1927 y que enunciaremos a continuación.

TEOREMA 3.16 (Mengen)

Un grafo G con p mayor o igual a n + 1 es n - conexo si y sólo si dos vértices cualesquiera u y v de G están conectados por al menos n caminos disjuntos por vértices.


Análogamente hay un teorema similar para las líneas.

TEOREMA 3.17

Un grafo G es n - linealmente conexo si y sólo si dos vértices cualesquiera de G están conectados por al menos n caminos disjuntos por líneas.