OPERACIÓN DE ELIMINACIÓN Y CONTRACCIÓN
La operación de eliminación abarca tanto las líneas como los vértices de un grafo G. Sea x una línea de G, denotaremos por G - x al grafo obtenido al eliminar de G la línea x. En general, si  es un subconjunto de n líneas de G, con n
es un subconjunto de n líneas de G, con n q, denotaremos con
q, denotaremos con  el grafo que se obtiene eliminando las n líneas que pertenecen a
el grafo que se obtiene eliminando las n líneas que pertenecen a 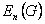 .
.
 es un subconjunto de n líneas de G, con n
es un subconjunto de n líneas de G, con n q, denotaremos con
q, denotaremos con  el grafo que se obtiene eliminando las n líneas que pertenecen a
el grafo que se obtiene eliminando las n líneas que pertenecen a 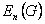 .
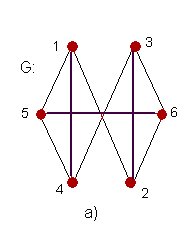
. Ejemplo 15: Para el grafo adjunto,
 ; G - x es el grafo obtenido después de eliminar de G la línea x (ver fig. 2.18 b)). Ahora, si
; G - x es el grafo obtenido después de eliminar de G la línea x (ver fig. 2.18 b)). Ahora, si
Análogamente, si v es un vértice de G, denotaremos por G - v, el grafo obtenido a partir de G por eliminación del vértice v, conjuntamente con todas sus líneas incidentes. En general, si 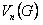 es cualquier subconjunto de n vértices de G, con n
es cualquier subconjunto de n vértices de G, con n 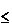 p, denotaremos con
p, denotaremos con 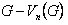 el grafo que se obtiene eliminando los vértices que están en
el grafo que se obtiene eliminando los vértices que están en 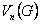 y todas sus líneas incidentes con cada uno de ellos.
y todas sus líneas incidentes con cada uno de ellos.
Ejemplo 16: Para el grafo de la fig. 2.24, si v es el vértice 2 de la figura; para G - v resulta el grafo de la fig. 2.19 b). Ahora, si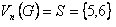 , el grafo obtenido es la parte c) de la misma figura.
, el grafo obtenido es la parte c) de la misma figura.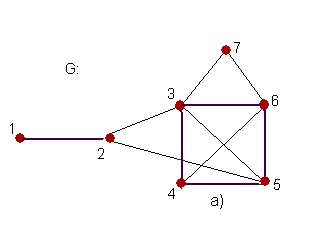


Por otra parte, la operación de contracción, que denotaremos con G \ x, siendo x una línea cualquiera del grafo, consiste en eliminar la línea x del grafo G y tomar sus vértices terminales, u y v, y unirlos, identificando uv. De esta forma, el vértice resultante uv es incidente a todas las líneas que eran originalmente incidentes con u y v (excluyendo a x).
del grafo, consiste en eliminar la línea x del grafo G y tomar sus vértices terminales, u y v, y unirlos, identificando uv. De esta forma, el vértice resultante uv es incidente a todas las líneas que eran originalmente incidentes con u y v (excluyendo a x).
Ejemplo 17: Sea G el grafo de la figura 2.20 a). Si x es la línea , entonces, el grafo G \ x resultante es el de la figura 2.20 b).
, entonces, el grafo G \ x resultante es el de la figura 2.20 b).
 del grafo, consiste en eliminar la línea x del grafo G y tomar sus vértices terminales, u y v, y unirlos, identificando uv. De esta forma, el vértice resultante uv es incidente a todas las líneas que eran originalmente incidentes con u y v (excluyendo a x).
del grafo, consiste en eliminar la línea x del grafo G y tomar sus vértices terminales, u y v, y unirlos, identificando uv. De esta forma, el vértice resultante uv es incidente a todas las líneas que eran originalmente incidentes con u y v (excluyendo a x).Ejemplo 17: Sea G el grafo de la figura 2.20 a). Si x es la línea
 , entonces, el grafo G \ x resultante es el de la figura 2.20 b).
, entonces, el grafo G \ x resultante es el de la figura 2.20 b).
 OBSERVACION 2.1.5: Al efectuar la contracción de algunos grafos, pueden aparecer líneas múltiples como es el caso del ejemplo 17, donde en realidad al hacer G \ x el grafo sería:
OBSERVACION 2.1.5: Al efectuar la contracción de algunos grafos, pueden aparecer líneas múltiples como es el caso del ejemplo 17, donde en realidad al hacer G \ x el grafo sería:
pero hay que recordar que para los efectos de esta guía, sólo consideramos grafos simples. En general, podemos decir que una contracción de G, es cualquier grafo que resulta a partir de G después de que se realiza una sucesión de eliminaciones de líneas con sus correspondientes contracciones. Por ejemplo, es una contracción del grafo de Petersen. En efecto, si a partir del grafo adjunto realizamos las contracciones sobre las líneas que unen a los vértices exteriores con los vértices interiores, llegaremos al
es una contracción del grafo de Petersen. En efecto, si a partir del grafo adjunto realizamos las contracciones sobre las líneas que unen a los vértices exteriores con los vértices interiores, llegaremos al como se muestra en la fig. 2.22.
como se muestra en la fig. 2.22.
 es una contracción del grafo de Petersen. En efecto, si a partir del grafo adjunto realizamos las contracciones sobre las líneas que unen a los vértices exteriores con los vértices interiores, llegaremos al
es una contracción del grafo de Petersen. En efecto, si a partir del grafo adjunto realizamos las contracciones sobre las líneas que unen a los vértices exteriores con los vértices interiores, llegaremos al como se muestra en la fig. 2.22.
como se muestra en la fig. 2.22.

1 Comments:
Amigo una pregunta las contracciones en vertices cmo se darian... gracias
Post a Comment
<< Home