JUEGOS DE INGENIO RELACIONADOS CON TEORÍA DE GRAFOS

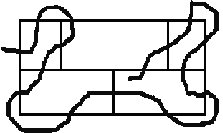
1.-EL CRUCE DE LA RED. Se trata de trazar una línea continua a través de la red cerrada de la figura mostrada, de modo que dicha línea cruce cada uno de los 16 segmentos que componen la red una vez solamente. La línea continua dibujada no es, evidentemente una solución del problema, ya que deja un segmento sin cruzar. Se ha dibujado solamente a fin de hacer patente el significado del enunciado del problema.

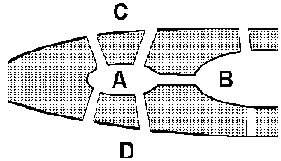
2.-LOS 7 PUENTES DE KONIGSBERG. Un ciudadano de Konigsberg (Prusia) se propuso dar un paseo cruzando cada uno de los siete puentes que existen sobre el río Pregel una sola vez. Los dos brazos del río rodean a una isla llamada Kneiphof. ¿Cómo debe cruzar los puentes para realizar el paseo?

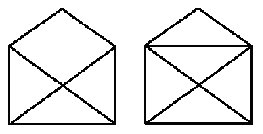
3.-DIBUJANDO SOBRES. En la figura tenemos dos sobres ligeramente diferentes ya que el segundo tiene una línea más, que marca la doblez de cierre. ¿Es posible dibujar cada uno de los sobres sin levantar el lápiz del papel, y sin pasar más de una vez por el mismo trazo?

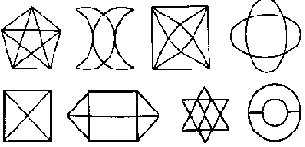
4.-EN GENERAL: DE UN SOLO TRAZO, ¿POSIBLE O IMPOSIBLE? Un vértice es impar si de el parten un número impar de caminos (valencia del vértice). Un vértice es par si de el parten un número par de caminos (valencia del vértice).

De los 8 dibujos de la figura, ¿cuáles pueden dibujarse de un sólo trazo y cuáles no?