GRAFO INTERSECCIÓN
Para una colección dada de conjuntos
Dos vértices de (S) están en relación si y sólo si los correspondientes conjuntos tienen una intersección no vacía, esto es,
(S) están en relación si y sólo si los correspondientes conjuntos tienen una intersección no vacía, esto es,
 (S) están en relación si y sólo si los correspondientes conjuntos tienen una intersección no vacía, esto es,
(S) están en relación si y sólo si los correspondientes conjuntos tienen una intersección no vacía, esto es,Entonces, un grafo G es un grafo intersección sobre S si existe una familia de subconjuntos de S para los cuales G es isomorfo con (S) .
(S) .
 (S) .
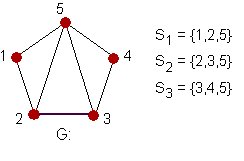
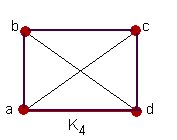
(S) . Ejemplo 2: Dado el grafo G de la fig. 2.4 y unos subconjuntos
 de vértices, hallar el grafo intersección de G.
de vértices, hallar el grafo intersección de G.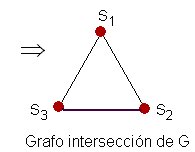 Figura 2.4
Figura 2.4Ejemplo 3: Dado el mismo grafo G de la fig. 2.4 y los siguientes subconjuntos 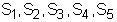 de líneas, hallar el grafo intersección de G.
de líneas, hallar el grafo intersección de G.
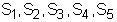 de líneas, hallar el grafo intersección de G.
de líneas, hallar el grafo intersección de G. Figura 2.5
Figura 2.5 TEOREMA 2.3 Todo grafo es un grafo intersección.
En vista del Teorema 2.3, tiene sentido definir el llamado número intersección i(G), para un grafo G, como el menor número de elementos en S para los cuales G es el grafo intersección sobre S .
COROLARIO 2: Si G es un grafo conexo y p 3, entonces: i(G)
3, entonces: i(G)  q.
q.
COROLARIO 2: Si G es un grafo conexo y p
 3, entonces: i(G)
3, entonces: i(G)  q.
q. La desigualdad es estricta en el Corolario 2, o sea que
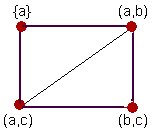
i(G) es menor o igual a q si y sólo si el grafo G no tiene triángulos como subgrafos. En efecto, consideremos 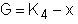 . G es isomorfo con
. G es isomorfo con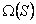 , donde S =
, donde S =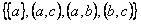 . Ver la fig. 2.6 que ilustra este hecho.
. Ver la fig. 2.6 que ilustra este hecho.
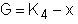 . G es isomorfo con
. G es isomorfo con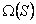 , donde S =
, donde S =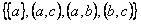 . Ver la fig. 2.6 que ilustra este hecho.
. Ver la fig. 2.6 que ilustra este hecho. Figura 2.6
Consideremos ahora una clase especial de grafos intersección llamados grafos clique. Clique de un grafo G es un máximo subgrafo completo de G, y el grafo clique, K(G), es el grafo intersección del conjunto de cliques de G, es decir,
Pero esta última igualdad no se cumple en general para todos los grafos como lo demuestra el ejemplo de la fig. 2.7, donde el grafo de la derecha es el grafo clique.
 Figura 2.7
Figura 2.7Veremos ahora operaciones que, habitualmente, se aplican sobre dos grafos, originando un tercero con propiedades y características propias.
En las próximas secciones de este capítulo los grafos G1 y G2 tendrán los conjuntos de vértices V(G1) y V(G2) disjuntos al igual que los conjuntos de líneas E(G1) y E(G2).


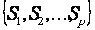

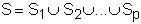
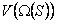










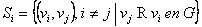


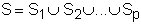
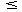




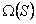
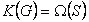

0 Comments:
Post a Comment
<< Home