SUMA O PRODUCTO UMBRAL DE DOS GRAFOS

Suma o producto umbral de dos grafos G1+G2

La suma o producto umbral de dos grafos, G1+G2, es una operación que consiste en la unión

G1G2 y de todas las líneas que unen V(G1) con V(G2). Esto es, u R v en G1+G2 si y sólo si

(u R v en G1) ó (u R v en G2)ó (u V(G1) y v V(G2)).

Ejemplo 7: La fig. 2.9 representa la suma de un y un .

Figura 2.9

Esta operación fue definida por el matemático ruso Zykov [Z1] y es particularmente útil para relacionar familias de grafos. Por ejemplo, el grafo bipartido puede escribirse como

+. También, la unión de grafos permite sintetizar la escritura de un grafo de n componentes isomorfas entre sí, en un grafo

.

Así, por ejemplo,

.

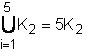Ejemplo 8: El grafo de la fig. 2.10, representa la suma umbral entre un 2 y un , entonces 2 + es un grafo regular de siete vértices y de valencia cuatro.

Figura 2.10

De la definición del producto umbral, es fácil deducir que y que , ya que G1+G2 tiene las líneas de G1, las de G2 y todas las posibles líneas que podemos tener desde G1 a G2; es decir, .

OBSERVACION 2.1.2: A continuación estudiaremos algunas operaciones con grafos, G1 y G2, las cuales resultan de considerar, como conjunto de vértices, el producto cartesiano de V(G1) y V(G2); esto es,