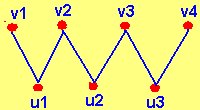
GRAFOS BIPARTIDOS

Otra clase de grafos que se presenta con frecuencia es la de los Grafos Bipartidos.

Un Grafo bipartito se denomina al grafo cuyos vértices se pueden separar en dos subconjuntos disjuntos V1(G) y V2(G) y las líneas siempre unen vértices de un subconjunto con vértices de otro subconjunto. Además se tiene que:

• V1(G) U V2(G) = V(G).
• La intersección de V1(G) y V2(G) es vacío.
• Para todos los puntos x1, x2 en V1(G) y para todos los puntos y1, y2 en V2(G) , no existe línea alguna x = (x1,x2) , ni x = (y1,y2).

A continuación, mostramos dos ejemplos de grafos bipartidos donde /V1(G)/ = 3 y /V2(G)/= 4

.

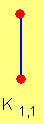
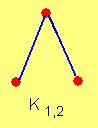
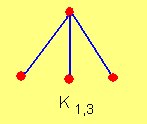
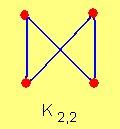
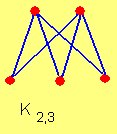
Un grafo bipartido en el cual todos los elementos de V1 están unidos con todos los elementos de V2 se denomina grafo bipartido completo.

El conjunto de los grafos bipartidos completos es denominado con la letra K. En particular, un grafo completo bipartido que une dos conjuntos, de m y n elementos respectivamente, se denota por Km,n. Es obvio que Km,n tiene p=(m+n) vértices y q=mn líneas.

.

Otro caso particular de los grafos bipartidos son los llamados Grafos Caminos o Serpientes, que se denotan Pp (Path), en donde :

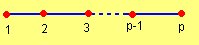
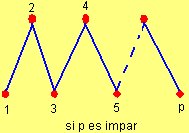
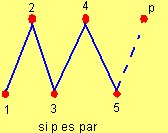
• V1(G) es {2, 4, ..., (p-1)} si p es impar ó {2, 4, ..., p} si p es par

• V2(G) es {1, 3, ..., (p-1)} si p es par ó {1, 3, ..., p} si p es impar

y las líneas son {n, n+1} para n = 1, 2, ..., p-1. Por lo tanto: val(1) = val(p) = 1 y val(i) = 2, si

..

.

Ejemplos:

.

.

También el Grafo Camino (Pp) , se puede dibujar así:

.

Otro caso particular es el grafo bipartido completo K1,p-1 , que se le suele llamar Estrella (también se puede denotar S1,p-1 (Start) ). Por ejemplo:

.

Un subgrafo de un grafo G es un grafo G' cuyo conjunto de vértices es un subconjunto del de G y cuyo conjunto de líneas es un subconjunto del conjunto de líneas de G.

De otra forma:

.
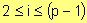
G' = (V',E') es un subgrafo de G = (V,E) si:

• G' es un grafo
• V' es un subconjunto de V
• E' es un subconjunto de E

.
Un subgrafo se obtiene eliminando puntos y líneas de un grafo. En particular, si seleccionamos un subconjunto S de vértices del Grafo G y le agregamos todas las líneas que unen dichos vértices en G, obtenemos un Subgrafo Inducido, que se denota .

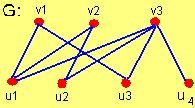
Ejemplo: El subgrafo formado por el conjunto de vértices S={u1, v2, u2, v3} es el subgrafo inducido <{u1, v2, u2, v3}>=C4 , en la siguiente figura:

.

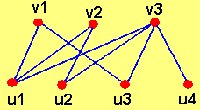
Otro subgrafo es el llamado Subgrafo Generador de G, el cual se obtiene tomando como subconjunto de vértices el conjunto de vértices V(G) de G, donde no es necesario que estén todas las líneas E(G) de G.

Un grafo H = (V',E') es un subgrafo de G = (V;A) si V' es subconjunto de V y si E' es subconjunto de E. Si V' = V, entonces H es un subgrafo generador de G.

La eliminación de un vértice de un grafo G es la forma más común de obtener un subgrafo de G, pero al eliminar un vértice se deben eliminar también, todas las líneas incidentes a él. Si eliminamos una línea "x", entonces, G-x es el grafo que resulta al eliminar dicha línea del grafo G. Por el contrario, si se agrega una línea cualquiera "x", entonces lo denotaremos G+x.