TEOREMA DE LAS VALENCIAS
La suma de las valencias de los vértices de un grafo es dos veces el número de líneas, es decir, si G es un grafo con "p" vértices y "q" líneas, entonces val(v1) + val(v2) + ... + val(vp) = 2q.
Demostración: Si vi pertenece a N(vj), entonces vj pertenece a N(vi), lo que implica que la línea (vi, vj) es contada dos veces. Como esto ocurre para cada vértice vi, con i entre 1 y p, la suma de todos los vi es 2q.
Corolario: En todo grafo G el número de vértices con valencia impar debe ser par.
Demostración: Los vi que pertenecen a V(G), con val(vi') par y los vi'' con val(vi'') impar.
Demostración: Los vi que pertenecen a V(G), con val(vi') par y los vi'' con val(vi'') impar.
Pero, la 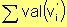 es par y 2q es un número par, lo que implica que la
es par y 2q es un número par, lo que implica que la  es la diferencia de dos números pares, y por lo tanto es par.
es la diferencia de dos números pares, y por lo tanto es par.
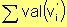 es par y 2q es un número par, lo que implica que la
es par y 2q es un número par, lo que implica que la  es la diferencia de dos números pares, y por lo tanto es par.
es la diferencia de dos números pares, y por lo tanto es par.Lo anterior es muy útil para verificar la existencia de grafos.
Por ejemplo, si tenemos los siguientes datos:
El grafo tiene 5 puntos, donde:
Val (1) = 2
Val (2) = 3
Val (3) = 1
Val (4) = 1
Val (5) = 4
Entonces no existe grafo alguno que cumpla con esta condición, pues viola el teorema anterior, ya que existen 3 puntos con valencia impar, y como vimos en la demostración la cantidad de vértices con valencia impar, debe ser par.
Por ejemplo, si tenemos los siguientes datos:
El grafo tiene 5 puntos, donde:
Val (1) = 2
Val (2) = 3
Val (3) = 1
Val (4) = 1
Val (5) = 4
Entonces no existe grafo alguno que cumpla con esta condición, pues viola el teorema anterior, ya que existen 3 puntos con valencia impar, y como vimos en la demostración la cantidad de vértices con valencia impar, debe ser par.
TEOREMA: Sea un grafo G = (p,q); entonces:
a) Si "p" es par, existen grafos regulares de cualquier valencia r, si
 .
.b) Si "p" es impar, existen grafos regulares solamente de valencia par r y si
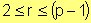 .
.Por ejemplo, si p = 7 existen grafos regulares de grado 2, 4 y 6



1 Comments:
Demostración del último teorema:
Dado que la valencia de cada vértice es r, la suma de ellas es p*r. Por Euler sabemos que p*r=2q. De aquí tenemos dos casos:
a) Si p es par, entonces no hay problemas con r, y tenemos que su valor puede variar entre 1 y p-1.
b) Si p es impar, entonces r debe ser par, y tenemos que su valor varía entre 2 y p-1 (no hay problema con p-1, pues es par).
QED
Post a Comment
<< Home