ISOMORFISMO DE GRAFOS
Definición:
Se dirá que dos grafos G y G' son isomorfos entre sí, si:

Donde V(G) = {1,2,3,4} y V(G') = {A,B,C,D} y como debe cumplirse que f:V(G)  V(G') es una biyección, entonces f(1) = D, f(2) = B, f(3) = C, f(4) = A. Observar que 1R4 en G, entonces, D R A en G'.
V(G') es una biyección, entonces f(1) = D, f(2) = B, f(3) = C, f(4) = A. Observar que 1R4 en G, entonces, D R A en G'.
Tenemos otra función que también define un isomorfismo entre G y G'.
f(1) = B, f(2) = D, f(3) = C y f(4) = A.
Observar, igualmente, que para este caso 1 R 4 en G, entonces, B R A en G'.
La relación de isomorfismo preserva las vecindades de cada vértice.
La relación de isomorfismo de dos grafos G y G' se denota de la siguiente manera, ![]()
- /V(G) /= /V(G')/
- /E(G) /= /E(G') /
- Si tiene vi tiene "k" vértices vecinos vi1, vi2, vi3, ... , vik, entonces, f(vi) tiene los siguientes "k" vértices vecinos f(vi1), f(vi2), f(vi3), ... , f(vik).
- vi y f(vi) tienen la misma valencia.

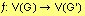
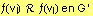

0 Comments:
Post a Comment
<< Home